| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 삼성 SDS 서포터즈
- 브라이틱스 서포터즈
- Brightics 서포터즈
- 브라이틱스 프로젝트
- 데이터 분석 플랫폼
- 브라이틱스 분석
- 브라이틱스 AI
- Python
- paper review
- 파이썬 내장 그래프
- 분석 툴
- Brightics AI
- Brigthics Studio
- 삼성 SDS
- michigan university deep learning for computer vision
- Brightics EDA
- 머신러닝
- 브라이틱스 스태킹
- 데이터 분석
- pymysql
- 검증 평가 지표
- Brightics studio
- Activation Function
- Random Forest
- 서포터즈 촬영
- 딥러닝
- 파이썬 SQL 연동
- 범주형 변수 처리
- 비전공자를 위한 데이터 분석
- Deep Learning for Computer Vision
- Today
- Total
하마가 분석하마
[Regularization model-1] Ridge Regression (1) 본문
[좋은 모델]
1) 현재 데이터를 잘 설명하는 모델
- training data를 잘 설명하는 모델로 training error를 최소화하는 모델이다.(MSE를 최소화하는 모델)
2) 미래 데이터에 대한 예측 성능이 좋은 모델
- E[MSE] = Irreducible Error + Bias^2 + Variance
- Irreducible Error : 모델로 어떻게 할 수 없는 에러
- Bias^2 + Variance : 모델로 어떻게 할 수 있는 에러
[Bias와 Variance]


- Expected MSE를 줄이려면 bias, variance 혹은 둘 다 낮춰야 함 (Bias와 Variance는 상충관계)
- 그렇지 못하다면 둘 중에 하나라도 작으면 좋음
- Bias가 증가되더라도 variance 감소폭이 더 크다면 expected MSE는 감소 (예측 성능 증가)
[Ordinary Linear Regression Model]
- Least squares method (최소제곱법) : 평균제곱오차 (MSE)를 최소화하는 회귀계수 B(beta)를 계산
- 최소제곱법은 회귀계수 beta에 대한 unbiased estimator 중 가장 분산이 작은 estimator (Best Linear Unbiased Estimator: BLUE, Gauss-Markov Theorem)

지금까지는 Bias 관점에서 아주 좋은 회귀계수 추정법이었다. (최소제곱법의 경우 bias를 선택하고 이후 variance를 선택하므로) 그렇다면 Bias estimator이지만 Variance를 굉장히 작게 하여 조금 더 효과를 볼 수 있지 않을까?
[Variance를 줄이는 법]
1. Subset Selection : 변수 선택
- Subset selection method는 전체 p개의 설명변수(X) 중 일부 k개만을 사용하여 회귀 계수 beta를 추정하는 방법
- 전체 변수 중 일부만을 선택함에 따라 bias가 증가할 수 있지만 variance가 감소함
- Best subset selection
- Forward stepwise selection
- Backward stepwise elimination
- Least angle regression
- Orthogonal matching pursuit
2. Regularization Concept : 정규화 개념
제약을 주는 관점

bias와 variance가 적당한 2번 모델이 좋지 않을까??
1번 모델에서 2번 모델로 가게 하기
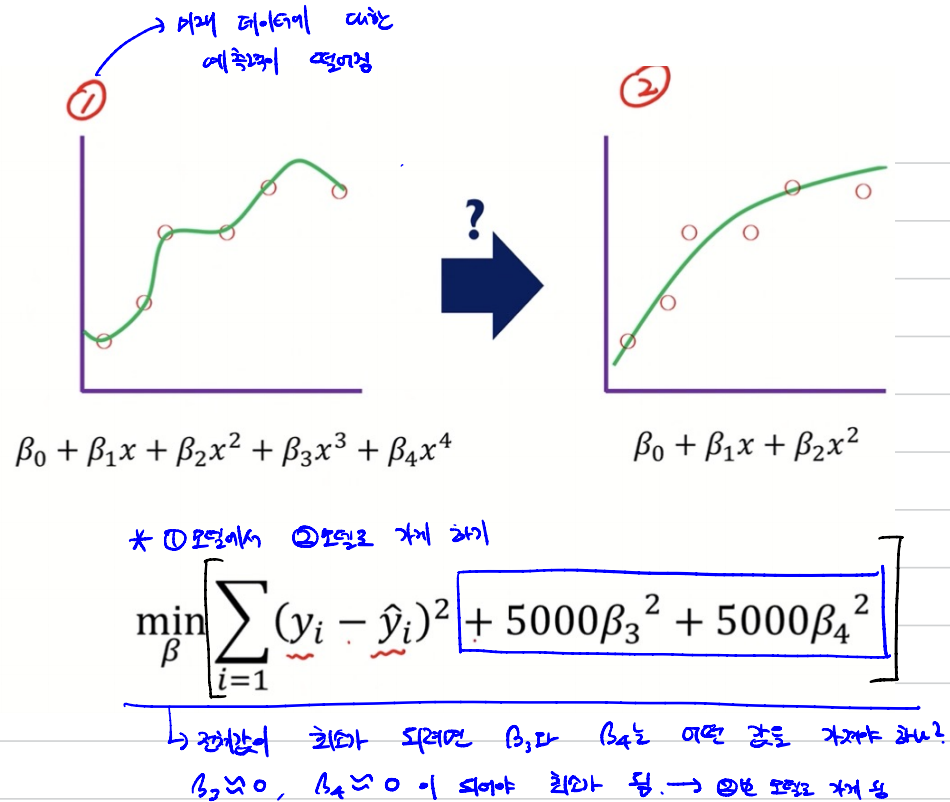
=> Training data에 너무 맞는 모델(1번)에 제약(정규화)을 두어, 미래 데이터를 보다 잘 예측하는 알고리즘을 사용
Beta가 1~p로 총 p개 있는 일반적인 모델의 loss 함수를 보자.

λ(람다)에 따른 변화


[정리]
- Regularization method는 회귀 계수 beta가 가질 수 있는 값에 제약조건을 부여하는 방법
- 제약조건에 의해 bias가 증가할 수 있지만 variance가 감소함

- ①번과 ➁번의 가장 큰 차이점은? : Beta에 대한 제약이 있는지와 없는지
- ① 방법은 unbiased를 맞추겠다는 Bias 관점
- ➁ 방법은 MSE도 고려는 하지만 Beta 값에 일정 제약을 둠으로써 Bias 뿐만 아니라 Variance도 고려하겠다는 뜻
[예제]

'알고리즘' 카테고리의 다른 글
| [Regularization model-1] Ridge Regression (2) (2) | 2021.06.06 |
|---|---|
| [Boosting] 4. XGBoost, Light GBM (0) | 2021.03.20 |
| [Bagging] 3. Random Forest-2 (0) | 2021.03.16 |
| [Bagging] 3. Random Forest-1 (0) | 2021.03.14 |
| [boosting] 2. GBM (0) | 2021.03.08 |




